Music is a language that transcends borders and cultures, a universal form of communication that can express what words sometimes cannot.
When we delve into the realm of music theory, one concept that often causes a bit of confusion is that of enharmonic equivalent notes and scales.
These are notes and scales that sound identical but are written differently, a small nuance with a significant impact on your understanding and interpretation of music.
To grasp this intriguing aspect of music, you must acquaint yourself with the way musicians think about sound and notation.
Enharmonic equivalents are like twins in music; they share the same pitch but carry different names depending on the context in which they’re used.
Recognizing these subtle differences not only helps you become a more versatile musician but also expands your capacity to communicate through the rich language of melodies and harmonies.
What are Enharmonic Equivalent Notes?
Enharmonic equivalent notes are pairs of notes that sound the same but are written differently.
In Western music notation, we often encounter these when dealing with sharp and flat notes.
For example, C sharp (C#) and D flat (Db) are enharmonic equivalents—they’re played on the same key on a piano but have different theoretical identities, which becomes essential in various musical contexts.
The concept hinges on the 12-tone equal temperament system where a semitone is the smallest interval, and each note has a potential twin elsewhere on the scale.
Understanding these nuances is crucial for reading and writing music accurately.
What is the Twelve-Tone Equal Temperament System?

The Twelve-Tone Equal Temperament System (12-TET) is a tuning standard that forms the foundation of Western music.
This system divides an octave into twelve pitches, each equally spaced in terms of frequency.
This equal spacing means that each pitch, called a semitone, is a fixed ratio apart from its neighbors.
Traditionally, musicians tuned instruments to just intonation, which emphasized pure intervals based on whole-number ratios.
However, this system had limitations when changing keys or modulating to different tonal centers.
In contrast, the 12-TET allows for consistent interval ratios across all keys, making it versatile for modern harmonies and enabling smooth key transitions without retuning.
As a result, pianos and other fixed-pitch instruments are commonly tuned using this system, facilitating their ability to play in any key with relative ease.
Understanding 12-TET is pivotal for musicians who wish to navigate through various musical genres and compositions without the constraints of tuning discrepancies among different keys.
Also Read: D Music Notes And Keys [Unraveling The Basics Of Guitar]
the Basics of Musical Notes
Music theory begins with a core building block: the note. Notes are the bedrock of melody and harmony, each one representing a specific pitch.
In Western music, there are seven basic note names, denoted by the first seven letters of the alphabet: A, B, C, D, E, F, and G. These notes form the foundation upon which scales and chords are built.
The Musical Staff and Notation
On written music sheets, these notes appear on a staff—a set of five horizontal lines where different pitches are notated.
To extend beyond these seven notes for higher or lower pitches, we use what’s called ledger lines to capture additional notes above or below the staff.
Sharps and Flats
To modify these base notes to different pitches we introduce accidentals: sharps (♯) and flats (♭). Sharps raise a note by a half-step while flats lower it by a half-step. For example:
- A sharp (^A♯^) is one half-step higher than A.
- E flat (^E♭^) is one half-step lower than E.
It’s crucial to understand that there’s also an invisible accidental known as the “natural,” which cancels any previous sharps or flats in a measure, ensuring that a note returns to its original pitch.
When approaching music theory, grasping these key elements provides you with essential tools for interpreting and creating music effectively.
Familiarizing yourself with this foundational vocabulary allows you to dive deeper into the world of enharmonic equivalents and understand their role within scales and harmonies.
By recognizing how pitches relate to each other through sharps and flats, you’re better equipped to understand scale structures which often involve patterns of whole steps (two half-steps) and half-steps, the smallest distance between two different pitches in Western music tradition.
Also Read: E Music Note Guide [Unlock Your Guitar’s Potential]
How Do Enharmonic Equivalents Affect Scales, Key Signatures, Chords, and Intervals?

Let’s take a journey into the nuanced world of enharmonic equivalents and understand their influence on various elements of music theory.
Scales: Building Blocks of Melody
Scales are the alphabets of the musical language from which melodies and harmonies are constructed.
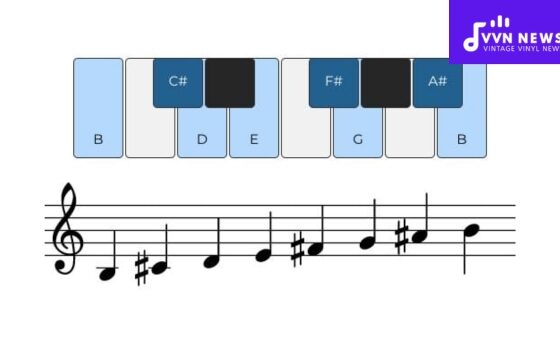
An enharmonic equivalent in a scale could change its entire identity. Take the scenario where we have a C sharp major scale (C#).
Now considering its enharmonic equivalent, you could also write this scale as a D flat major (Db) scale. While C# and Db sound the same when played, they are notated differently:
- C# Major: C#, D#, E#, F#, G#, A#, and B#
- Db Major: Db, Eb, F, Gb, Ab, Bb, and C
Both scales sound identical but use different note spellings.
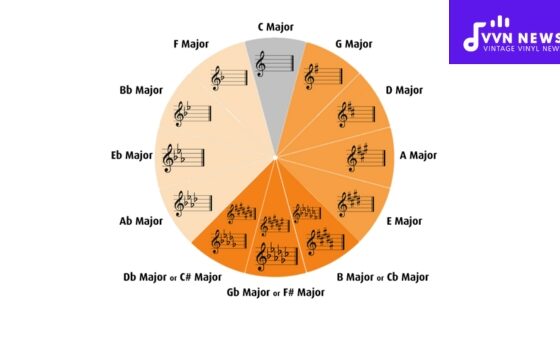
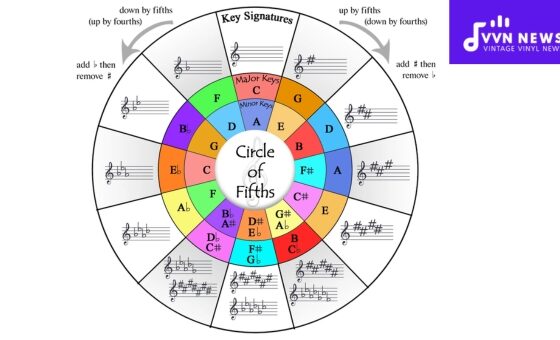
Key Signatures: The Musical Context
Key signatures set the tonal landscape for pieces of music by indicating which notes are to be consistently sharpened or flattened throughout a composition.
If you’re working with an instrument like a piano or guitar that doesn’t change tuning systems between keys, recognizing enharmonic key signatures is essential for streamlining readings and transpositions.
For instance, consider the key signature for G flat major with six flats; it is enharmonically equivalent to F sharp major with six sharps even though visually quite distinct.
Chords: Harmonic Expressions
Chords consist of multiple notes played simultaneously to express harmony within the music.
With chords often being built upon scales, enharmonic equivalents play their part here too.
An E flat chord built upon an E flat major scale can equally be enunciated as a D sharp chord based on a D sharp scale – albeit rather rare in notational practice due to potentially complex spelling.
Intervals: The Spaces Between
Intervals the distance between two notes, likewise feel the ripple effects of harmonics.
The interval between C and E is known as a major third, but if you were to spell it between C and Fb (enharmonically the same as E), theoretically, you’ve created an augmented fourth.
Enharmonics can seem perplexing at first glance, but remember, they offer flexibility in how we perceive sounds within our music system, not altering pitches but changing their notational perspective.
Understanding these concepts deepens our analytical skills in music theory while providing practical advantages during performance practice, ensuring that we connect more profoundly with this incredible art form.
Also Read: D Flat Music Note [Cracking The Code Of Musical Notation]
Enharmonic Usage in Historical Context
Before the Romantic period, music was governed by modal systems and the meantone temperament, which influenced how enharmonic equivalents were perceived and utilized.
Instruments such as the clavichord allowed performers to express subtle differences between enharmonically equivalent notes due to their flexible tuning systems.
Composers of the Renaissance and Baroque eras frequently employed enharmonic equivalents as a means of modulation or to add expressive chromaticism to their works, but always within the bounds of the tuning systems of their time.
Notably, in these periods, an F-sharp might not sound identical to a G-flat as they do on modern pianos; each had its place and purpose, reflective of a musical structure that favored purity of intervals based on just intonation a system where intervals are derived from whole number ratios.
Enharmonic shifts were often used for dramatic effect or to ease technical execution in vocal and instrumental compositions.
As we transitioned into the Romantic period with advancements in instrument construction and tuning methods, these nuances gave way to our current understanding, where these notes often sound indistinguishable.
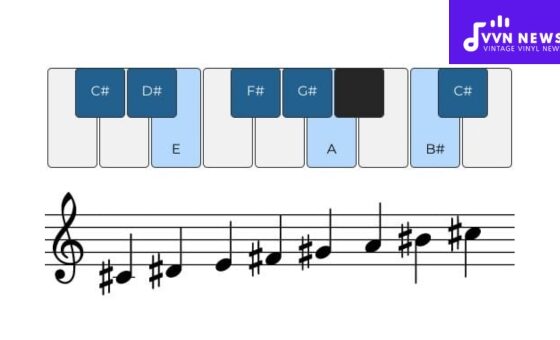
How To Represent a Chromatic Scale?

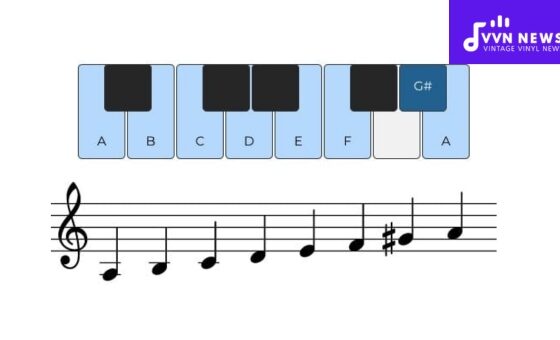
One of the foundational elements in music theory is the chromatic scale, a sequence that includes all twelve pitches available within an octave.
Each pitch is a half step, or semitone, away from its neighbors. Here’s how you can represent a chromatic scale effectively:
- Start with Note C: While you could start on any note, C is commonly used as it is a natural starting point in the diatonic system.
- Ascend by Semitones: From C, move up each semitone. After C comes C#, then D, and so forth.
- Use Sharps and Flats: When ascending the scale, sharps are typically used; when descending, flats are favored. However, context determines whether you use a sharp or flat for enharmonic equivalents. For instance, G# in one key might be Ab in another.
- Include All Notes: Ensure your chromatic scale includes all seven natural notes (A B, C D E F G) and all five accidental notes (C# or Db, D# or Eb, F# or Gb, G# or Ab, A# or Bb).
- Return to the Root Note: Finish your scale by returning to C above your starting note.
Representing a chromatic scale in notation requires understanding key signatures to determine whether flats or sharps are appropriate at any given location within the score.
A composer decides, based on key signature constraints and melodic flow, which enharmonic spellings to use.
Also Read: C Sharp Major Pentatonic Scale [Crisp & Clear Tones For Your Music]
FAQs About Enharmonic Equivalent Notes and Scales
What exactly does ‘enharmonic equivalent’ mean in music?
Enharmonic equivalents are two notes that sound the same but are represented by different note names, such as C# and Db.
Can you give another example of enharmonic equivalent notes?
Sure, an example would be G# and Ab; they sound identical on a piano but are written differently depending on the musical context.
How do enharmonic equivalents affect tuning?
In modern tuning systems like equal temperament, enharmonic equivalents are tuned to the same pitch, which simplifies instrument design and playing.
Why are enharmonic equivalents important in compositions?
Enharmonic equivalents allow composers to modulate between keys more smoothly and to write music that is easier for musicians to read and interpret.
When reading music, how do I know which enharmonic note to play?
The key signature and context within the musical piece will guide you in choosing the correct enharmonic notation.
Conclusion
In the intricate tapestry of music theory, enharmonic equivalent notes and scales stand out as a fascinating element that adds depth and flexibility to musical expression.
By understanding that a note like C-sharp can be the same in pitch as D-flat, you unlock new doors to interpretative possibilities across diverse musical genres.
While they might look different on paper or your screen, enharmonic equivalents are aurally identical, creating seamless transitions in your music-making journey.